그래프
그래프는 요소들이 서로 연결되어 있는 관계를 표현한 자료구조이다. 그래프는 정점(vertex)와 그들을 연결하는 간선(edge)의 집합으로 구성된다. 수학적으로는 다음과 같이 표시한다.
(\G = (V, E)\)
\(V(G)\)는 그래프 \(G\)의 정점의 집합, \(E(G)\)는 그래프 \(G\)의 간선의 집합
정점 A와 정점 B가 있다고 하면, 두 정점을 이어주는 간선은 (A, B)와 같이 정점의 쌍으로 나타낸다. 그래프는 정점과 간선의 집합이기 때문에, 한 그래프를 그리는 방법은 다양하다.



무방향 그래프(undirected graph)
간선에 방향이 표시되지 않은 그래프이다. 두 정점 A, B에 대하여 간선 (A, B)와 (B, A)는 동일한 간선이 된다. 현실의 것과 비유하자면, 지하철 노선도와 비슷한 형태이다.



방향 그래프(directed graph)
간선에 방향이 있는 그래프이다. 화살표로 표현해서, 그 간선은 그 방향으로만 갈 수 있다고 나타낸다. 두 정점 A, B에 대하여 A에서 B로 갈 수 있는 간선은 <A, B>로 나타낸다. 무방향 그래프와는 달리 <A, B>와 <B, A>는 다른 간선이다. 도로에서 일방통행 도로와 마찬가지로 한 방향으로만 갈 수 있다.



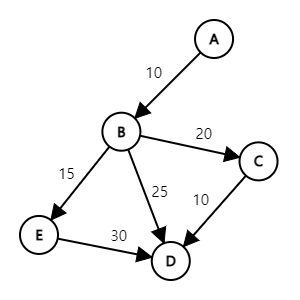
가중치 그래프(weighted graph)
간선에 가중치라는 값이 할당된 그래프이다. 도시 사이의 도로와 그 길이를 표현해 최단 거리를 구하는 등 다양한 곳에서 응용될 수 있다.


그래프 용어

인접 정점(adjacent vertex) : 간선으로 직접 연결된 정점. 위 그림에서 정점 0의 인접 정점은 2, 4, 5이다.
정점의 차수(degree) : 그 정점에 연결된 간선의 수. 무방향 그래프에서는 인접 정점의 수와 같다. 방향 그래프에서는 한 정점으로 외부에서 들어오는 간선의 수를 진입 차수(in-degree), 외부로 나가는 간선을 진출 차수(out-degree)라고 한다.
경로(path) : 간선을 따라 갈 수 있는 길. 정점들의 나열로 표시한다. 위 그래프에서 0, 2, 3은 경로가 될 수 있지만, 1, 4, 3은 경로가 될 수 없다. 간선 (3, 4)가 없기 때문이다.
사이클(cycle) : 같은 간선을 다시 지나지 않으면서, 출발한 정점으로 다시 돌아오는 경로. 0, 4, 2, 0은 사이클이다.
연결 그래프(connected graph) : 모든 정점들 사이에 경로가 존재한 그래프. 그렇지 않으면 비연결 그래프라고 한다.
트리(tree) : 사이클을 가지지 않는 연결 그래프. 앞에서 공부한 그 트리이다. 즉. 트리는 그래프의 특수한 형태 중 하나이다.
완전 그래프(complete graph) : 모든 정점들 사이에 간선이 존재하는 그래프이다. 완전 그래프에서는 정점의 수가 \(n\) 이라면 한 정점이 가지는 간선의 수는 \(n - 1\) 이 되고, 모든 간선의 수는 \(n \times (n-1) / 2\) 가 된다.
그래프의 구현
[인접 행렬] 그래프 구현
그래프의 정점의 수를 n이라고 하면 n x n 의 2차원 배열에 저장하는 방식이다. 행렬 M과 정점 i와 j가 주어지면 간선 (i, j)를 다음과 같이 표현한다.
M[i][j] = 가중치;대각선 성분은 모두 0으로 초기화시켜준다. 이 외의 연산들은 앞의 자료구조를 직접 구현해 봤다면 크게 어려운 부분이 없다.
#include <iostream>
#include <vector>
const int MAX_VTX = 16;
const int INF = 9999999;
class Array_Graph {
int grp[MAX_VTX][MAX_VTX];
int vtxsize;
char vtx[MAX_VTX];
public:
Array_Graph() {
vtxsize = 0;
for (int i = 0; i < MAX_VTX; i++) {
for (int j = 0; j < MAX_VTX; j++) {
grp[i][j] = INF;
}
vtx[i] = NULL;
}
}
bool is_empty() { // 공백 검사
return vtxsize == 0;
}
bool is_full() { // 포화 검사
return vtxsize == MAX_VTX;
}
void insert_vertex(char m_vtx) { // 정점 삽입
vtx[vtxsize] = m_vtx;
vtxsize++;
}
void insert_edge(int to, int from, int val = 1) { // 간선 삽입(방향)
grp[to][from] = val;
}
void insert_edge_u(int v1, int v2, int val = 1) { // 간선 삽입(무방향)
grp[v1][v2] = grp[v2][v1] = val;
}
void print() {
cout << "정점의 수 : " << vtxsize << endl;
for (int i = 0; i < vtxsize; i++) {
cout << "\t" << vtx[i];
}
cout << endl;
for (int i = 0; i < vtxsize; i++) {
cout << vtx[i];
for (int j = 0; j < vtxsize; j++) {
cout << "\t" << grp[i][j];
}
cout << endl;
}
}
};
int main() {
Array_Graph ag;
for (int i = 0; i < 4; i++) {
ag.insert_vertex('A' + i); // A B C D
}
ag.insert_edge_u(0, 1);
ag.insert_edge_u(0, 3);
ag.insert_edge_u(1, 2);
ag.insert_edge_u(1, 3);
ag.insert_edge_u(2, 3);
ag.print();
return 0;
}
[인접 리스트] 그래프 구현
인접 리스트를 이용한 방법도 다른 방법들 처럼 그래프 노드 구조체를 선언해준다.
struct GrpNode {
int id;
int weight;
GrpNode* link;
};
GrpNode* grp[MAX_VTX];weight는 간선의 가중치를 저장한다. grp는 각 정점들의 헤더 포인터를 저장하는 배열이다. 즉, grp[i]는 i번째 정점의 인접 리스트에 대한 헤더 포인터로, 그 헤더 포인터를 따라가면 연결된 노드들을 알 수 있다.
나머지 연산은 인접 행렬과 비슷하다.
#include <iostream>
#include <queue>
const int MAX_VTX = 16;
const int INF = 9999999;
class Linked_Graph {
struct GrpNode {
int id;
int weight;
GrpNode* link;
};
GrpNode* grp[MAX_VTX];
int vtxsize;
char vtx[MAX_VTX];
public:
Linked_Graph() {
vtxsize = 0;
for (int i = 0; i < MAX_VTX; i++) {
grp[i] = NULL;
}
}
bool is_empty() { // 공백 연산
return vtxsize == 0;
}
bool is_full() { // 포화 연산
return vtxsize == MAX_VTX;
}
void reset_graph() { // 그래프 초기화
GrpNode* n;
for (int i = 0; i < vtxsize; i++) {
while (grp[i] != NULL) {
n = grp[i];
grp[i] = n->link;
delete n;
}
}
vtxsize = 0;
}
void insert_vertex(char m_vtx) { // 정점 추가
vtx[vtxsize] = m_vtx;
vtxsize++;
}
void insert_edge(int v1, int v2, int w = 1) { // 간선 추가(방향)
GrpNode* n = new GrpNode;
n->link = grp[v1];
n->id = v2;
n->weight = w;
grp[v1] = n;
}
void insert_edge_u(int v1, int v2, int w = 1) { // 간선 추가(무방향)
GrpNode* n = new GrpNode;
n->link = grp[v1];
n->id = v2;
n->weight = w;
grp[v1] = n;
n->link = grp[v2];
n->id = v1;
n->weight = w;
grp[v2] = n;
}
void print() {
cout << "정점의 수 : " << vtxsize << endl;
for (int i = 0; i < vtxsize; i++) {
cout << vtx[i];
for (GrpNode* n = grp[i]; n != NULL; n = n->link) {
cout << "\t" << vtx[n->id];
}
cout << endl;
}
}
};
void lgrp_test() {
Linked_Graph lg;
for (int i = 0; i < 4; i++) {
lg.insert_vertex('A' + i); // A B C D
}
lg.insert_edge_u(0, 1);
lg.insert_edge_u(0, 3);
lg.insert_edge_u(1, 2);
lg.insert_edge_u(1, 3);
lg.insert_edge_u(2, 3);
lg.print();
}
그래프를 이용한 알고리즘은 다양하다. 이 다양한 알고리즘들은 알고리즘 카테고리에서 다루도록 하겠다.
[Reference]
자료구조 - 교보문고
컴퓨터로 어떤 문제를 해결하기 위해 필요한 자료들을 효율적으로 관리하고 구조화시키기 위한 학문 '자료구조'. 이 책은 자료구조를 보다 명확하게 배울 수 있도록 구성되어 있다. 각 장에서는
www.kyobobook.co.kr
'알고리즘(Algorithm) > Data Structure' 카테고리의 다른 글
| [자료구조] 우선순위 큐와 힙 (0) | 2022.03.15 |
|---|---|
| [자료구조] 트리 (0) | 2022.03.14 |
| [자료구조] 큐 (0) | 2022.03.04 |
| [자료구조] 스택 (0) | 2022.03.02 |