미숙한 블로그 주인이 코딩테스트 문제를 풀어가는 과정을 담은 글입니다. 이 풀이가 효율적인 풀이가 아닐 수 있으며, 부정확한 정보가 많이 있을 수 있습니다. 보완해야할 점이 있다면 댓글로 남겨주세요!
https://programmers.co.kr/learn/courses/30/lessons/42861
코딩테스트 연습 - 섬 연결하기
4 [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 4
programmers.co.kr
섬 연결하기
문제
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한사항
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는 ((n-1) * n) / 2이하입니다.
- 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
- 연결할 수 없는 섬은 주어지지 않습니다.
풀이
입출력 예시
입출력 예
ncostsreturn
4 [[0,1,1],[0,2,2],[1,2,5],[1,3,1],[2,3,8]] 4 입출력 예 설명
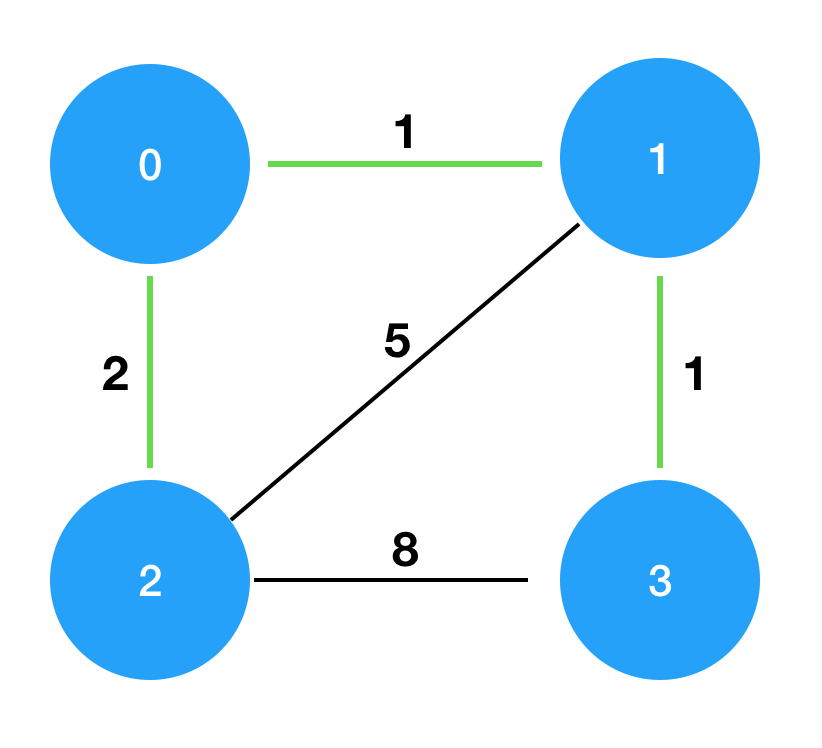
costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.
풀이
문제를 이해 했거나, 입출력 예의 사진을 봤다면 이 문제는 최소 신장 트리를 구하는 문제임을 바로 알 수 있다. 최소 신장 트리는, 가중치 그래프에서 가중치들의 합이 최소가 되는 트리이다.
문제의 분류도 힌트가 될 수 있는데, 최소 신장 트리를 구하는 데 필요한 알고리즘들인 프림 알고리즘과 크루스칼 알고리즘은 대표적인 그리디 알고리즘이기 때문이다.
간편하게 프림 알고리즘을 이용해서 풀었다.
#include <string>
#include <vector>
using namespace std;
const int INF = 9999999;
int get_min_vertex(vector<bool> selected, vector<int> dist, int n) {
int mindist = INF;
int minv = 0;
for (int v = 0; v < n; v++) {
if (selected[v] == false && dist[v] < mindist) {
mindist = dist[v];
minv = v;
}
}
return minv;
}
int solution(int n, vector<vector<int>> costs) {
int answer = 0;
vector<bool> selected(n);
vector<int> dist(n, INF);
vector<vector<int>> grp(n, vector<int>(n, INF));
for (const auto& cost : costs) {
grp[cost[0]][cost[1]] = cost[2];
grp[cost[1]][cost[0]] = cost[2];
}
selected[0] = true;
dist[0] = 0;
for (int i = 0; i < n; i++) {
int u = get_min_vertex(selected, dist, n);
selected[u] = true;
for (int v = 0; v < n; v++) {
if(grp[u][v] != INF) {
if (selected[v] == false && grp[u][v] < dist[v]) {
dist[v] = grp[u][v];
}
}
}
}
for (const auto& d : dist) {
answer += d;
}
return answer;
}
'코딩 테스트(Coding test) > Lv. 3' 카테고리의 다른 글
| [프로그래머스/C++] 단속카메라 (0) | 2022.06.27 |
|---|---|
| [프로그래머스/C++] 최적의 행렬 곱셈 (0) | 2022.06.27 |
| [프로그래머스/C++] [1차] 추석 트래픽 (0) | 2022.06.26 |
| [프로그래머스/C++] 표 편집 (0) | 2022.06.24 |
| [프로그래머스/C++] 불량 사용자 (0) | 2022.06.14 |