10개의 원소를 갖는 아래와 같은 배열이 있다. 이 배열에서 i번째의 값을 찾는다고 해보자.
arr[10] = { 10, 2, 5, 7, 6, 4, 8, 1, 9, 3 }우선 배열을 한 번씩은 다 훑어봐야 하므로 적어도 n에 비례하는 시간이, 즉 \(\Omega(n)\)이 될것이다. 정렬을 한다면 \(O(nlogn)\)일 것이다. 어떤 시간에서든 선형 시간에 가능하도록 보장해줄 수 있도록 하는 알고리즘이 없을까? 이를 가능하도록 하는 알고리즘이 바로 선형 시간 선택 알고리즘이다.
평균 선형 시간 선택 알고리즘
선택 알고리즘은 퀵 정렬에서 사용했던 분할 알고리즘을 사용한다. 위의 경우에서 분할 알고리즘을 사용한다면 i번째 값을 찾을 수 있다. 기준원소를 5로 하고, 3번째로 작은 원소를 찾는다고 해보자. 분할 알고리즘을 통해 5는 5번째 수 임을 알 수가 있다.
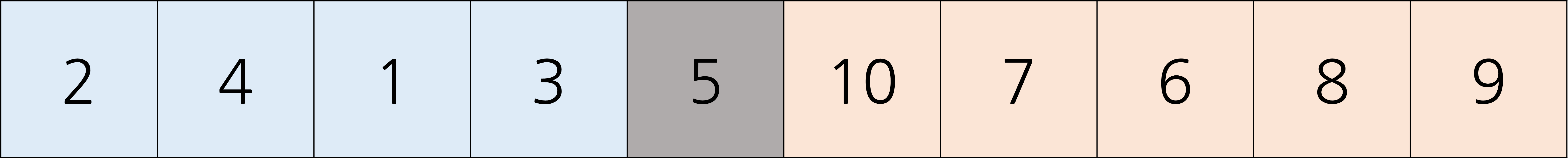
5가 5번째로 작은 원소이므로, 3번째로 작은 원소는 5의 왼쪽에 위치한다. 5의 왼쪽에 있으므로 오른쪽 부분은 볼 필요가 없어졌다. 이제 왼쪽에서 3번째로 작은 원소를 찾아야한다. 이번에는 2를 기준으로 분할을 해보자. 이때, 오른쪽은 더 이상 분할을 할 필요가 없다는 것을 상기하자.
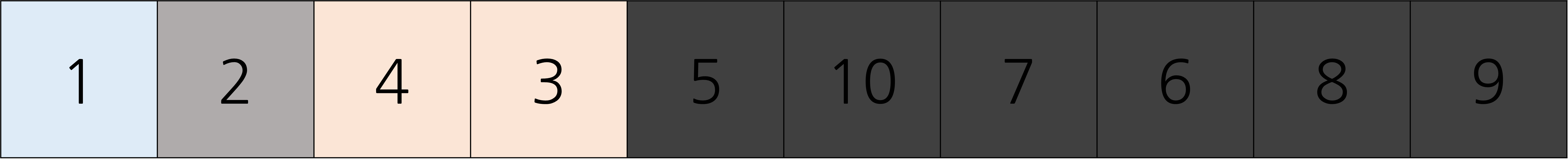
2는 2번째로 작은 원소임을 알았다. 3번째로 작은 원소는 이제 2의 오른쪽 부분에서 1번째로 작은 원소일 것이다. 이 과정을 반복하며 값을 찾아내면 3이라는 원소가 나온다. 이를 코드로 옮기면 아래와 같다.
int avg_select(int arr[], int start, int end, int n) {
int pivot; // 기준 원소
int p_order; // 기준 원소가 몇 번째 원소인지
if (start == end) { // 원소 하나만 찾는 것
return arr[start];
}
pivot = partition1(arr, start, end); // 퀵 정렬에서 사용한 partition과 동일
p_order = pivot - start + 1;
if (n < p_order) {
return avg_select(arr, start, pivot - 1, n);
}
else if (n > p_order) {
return avg_select(arr, pivot + 1, end, n - p_order);
}
else {
return arr[pivot];
}
}실행 시간은 다음과 같다.
$$\begin{flalign}T(n) \le \max[T(k-1),T(n-k)]+\theta(n)&&\end{flalign}$$
위의 식을 평균내면 \(\Theta(n)\)의 시간이 걸린다. 하지만 퀵 정렬에서의 예시에서도 그랬듯, 항상 기준 원소가 최대 혹은 최소가 선택된다면 \(\Theta(n^2)\)의 시간이 소요된다. 이 단점을 개선하기 위한 알고리즘이 다음에 나오는 알고리즘이다.
[+] 평균적으로 \(\Theta(n)\)인 이유
기준원소가 \(k\)번째 원소라고 하자. 그렇다면 그룹은 각각 \(k - 1\)과 \(n - k\)으로 나뉜다.
\(T(n) \le \max[T(k-1), T(n-k)]+\Theta(n)\)
이 식의 평균을 구해보자.
$$\begin{flalign} T(n) &\le \frac{1}{n}\sum_{k=1}^n \max[T(k-1),T(n-k)]+\Theta(n) \\&\le \frac{2}{n}\sum_{k=\lfloor{n \over 2}\rfloor}^{n-1}T(k)+\Theta(n) && \end{flalign}$$
\(\lfloor{n \over 2}\rfloor \le k < n \)인 모든 \(k\)에 대해 \(T(k) \le ck\)라고 가정한다면,
$$\begin{flalign} T(n) &\le {2 \over n}\sum_{k=\lfloor{n \over 2}\rfloor}^{n-1}ck + \theta(n) \\&={2 \over n}(\sum_{k=1}^{n-1}ck - \sum_{k=1}^{\lfloor{n \over 2}\rfloor-1}ck) + \theta(n) \\&= {2 \over n}({c(n-1){n \over 2}}-{c(\lfloor {n \over 2} \rfloor-1) \lfloor {n \over 2} \rfloor \over 2})+\theta(n) \\&\le {2c \over n}({n(n-1) \over 2}-{({n \over 2}-2)({n \over 2}-1) \over 2})+\theta(n) \\&= c(n-1)-{c \over n}({n^2 \over 4}-{3n \over 2}+2)+\theta(n) \\&= cn+(-{cn \over 4}+{c \over 2}-{2c \over n} + \theta(n)) && \end{flalign}$$
\(cn \ge cn+(-{cn \over 4}+{c \over 2}-{2c \over n} + \theta(n))\)를 만족하는 상수\(c\)가 존재한다.
\(∴ T(n) = O(n)\)
\(T(n) = \Omega(n)\)이기도 하므로 \(T(n) = \Theta(n)\)이다.
최악의 경우에도 선형 시간을 보장하는 선택 알고리즘
제목이 조금 긴데, 쉽게 말해서 항상 기준 원소를 최대(혹은 최소)로 잡지 않도록 하겠다는 뜻이다. 다시 분할의 경우를 보자. 분할이 계속해서 1:9로 되고, 항상 9인 부분에서 탐색을 지속한다고 하자. 그렇다면 수행 시간은 아래와 같을 것이다.
$$\begin{flalign}T(n) = T({9 \over 10}n) + \Theta(n) &&\end{flalign}$$
이를 계산하면 \(T(n) = \Theta(n)\)이 된다.
[+] \(T(n) = \Theta(n)\) 유도
\(\Theta(n) = cn, n = {1 \over k}\)로 가정하자.
$$\begin{flalign}T(n) &\le T({9 \over 10}n) + cn \\ &\le {1 \over 2}T({9 \over 10}2n) + 2cn \\ &\le {1 \over 3}T({9 \over 10}3n) + 3cn \\ &\vdots \\ &\le {1 \over k}T({9 \over 10}kn) + kcn \\ &\le nT({9 \over 10}) +c \\ &\le cn &&\end{flalign}$$
$$\begin{flalign}\therefore T(n) = \Theta(n) &&\end{flalign}$$
1:99로 분할된다고도 해보자. 그렇다면 \(T(n)\)은 아래와 같을 것이다.
$$\begin{flalign}T(n) = T({99 \over 100}n) + \Theta(n) &&\end{flalign}$$
이를 계산하면 마찬가지로 \(T(n) = \Theta(n)\)이 된다.
즉, 분할되는 비율이 좋지 않아도 어떻게든 일정 비율까지만 보장해준다면 최악의 경우에도 \(\Theta(n)\)을 보장해줄 수 있다. 물론 분할이 일정 비율을 유지하도록 하는 오버헤드가 너무 커져버리면 목표를 이룰 수 없다.
그렇다면 이 방법은 어떻게 작동하는 것일까? 아래와 같은 경우를 반복한다.
arr이라는 배열에서 i번째 작은 원소를 찾는다고 하자.
1. 원소의 총 수가 5개 이하이면 i번째 원소를 찾고 반환한다.
2. 전체 원소를 5개씩 원소를 가진 \(\lceil {n \over 5} \rceil \)개의 그룹으로 나눈다.
( 원소의 수가 5의 배수가 아니면 하나의 그룹은 원소가 5개 미만이다. )
3. 각 그룹에서 중앙값을 찾는다. 이 중앙값들을 \(m_1, m_2, \cdots, m_{\lceil {n \over 5} \rceil} \)이라고 하자.
4. 재귀 호출로 \(m_1, m_2, \cdots, m_{\lceil {n \over 5} \rceil} \)들의 중앙값 \(M\)을 구한다.
( 만약 중앙값들이 짝수개이면 임의로 하나를 선택한다.)
5. \(M\)을 기준 원소로 해서 전체 원소를 분할한다.
6. 분할된 부분에서 적합한 부분을 선택한다.
7. 1~6을 반복한다.
#include <algorithm>
#include <vector>
using namespace std;
int search_median(vector<int> &arr, int start, int end);
int get_median(vector<int>& arr, int start, int end);
int partition(vector<int>& arr, int start, int end, int pivot);
int linear_select(vector<int> arr, int start, int end, int n) {
int med; // 중앙값
int pivot; // 기준 원소
int p_order; // 기준 원소가 몇 번째 원소인지
if (start == end) { // 원소 하나만 찾는 것
return arr[start];
}
med = get_median(arr, start, end);
pivot = partition(arr, start, end, med);
p_order = pivot - start + 1;
if (n < p_order) {
return worst_case_select(arr, start, pivot - 1, n);
}
else if (n > p_order) {
return worst_case_select(arr, pivot + 1, end, n - p_order);
}
else {
return arr[pivot];
}
}
// 중앙값을 구한다.
int search_median(vector<int> &arr, int start, int end) {
int mid = (start + end) / 2;
sort(arr.begin(), arr.end());
return arr[mid];
}
int get_median(vector<int> &arr, int start, int end) {
vector<int> median_list; // 중앙값을 저장할 벡터
vector<vector<int>> group; // 그룹
vector<int> temp; // 그룹에 넣기 위한 임시 변수
if ((end - start) < 5) {
return search_median(arr, start, end);
}
// 전체 원소를 5개씩의 원소를 가진 ceil(n/5)개의 그룹으로 나눈다.
for (int i = start; i <= end; i += 5) {
for (int j = i; j < i + 5 && j <= end; j++) {
temp.push_back(arr[j]);
}
group.push_back(temp);
temp.clear();
}
// 각 그룹에서 중앙값을 찾는다.
for (auto& g : group) {
median_list.push_back(search_median(g, 0, g.size() - 1));
}
// 재귀 호출로 중앙값들의 중앙값을 구한다.
if (median_list.size() == 1) {
return median_list[0];
}
else {
return get_median(median_list, 0, median_list.size() - 1);
}
}
int partition(vector<int> &arr, int start, int end, int pivot) {
int idx = start - 1; // 기준보다 작은 원소의 수
int p_idx = 0; // 기준의 인덱스
for (int i = start; i <= end; i++) {
if (arr[i] < pivot) {
idx++;
swap(arr[idx], arr[i]);
}
if (arr[i] == pivot) {
p_idx = i;
}
}
idx++;
swap(arr[idx], arr[p_idx]);
return idx;
}최악의 경우에도 \(T(n) = \Theta(n)\)를 보장해준다.
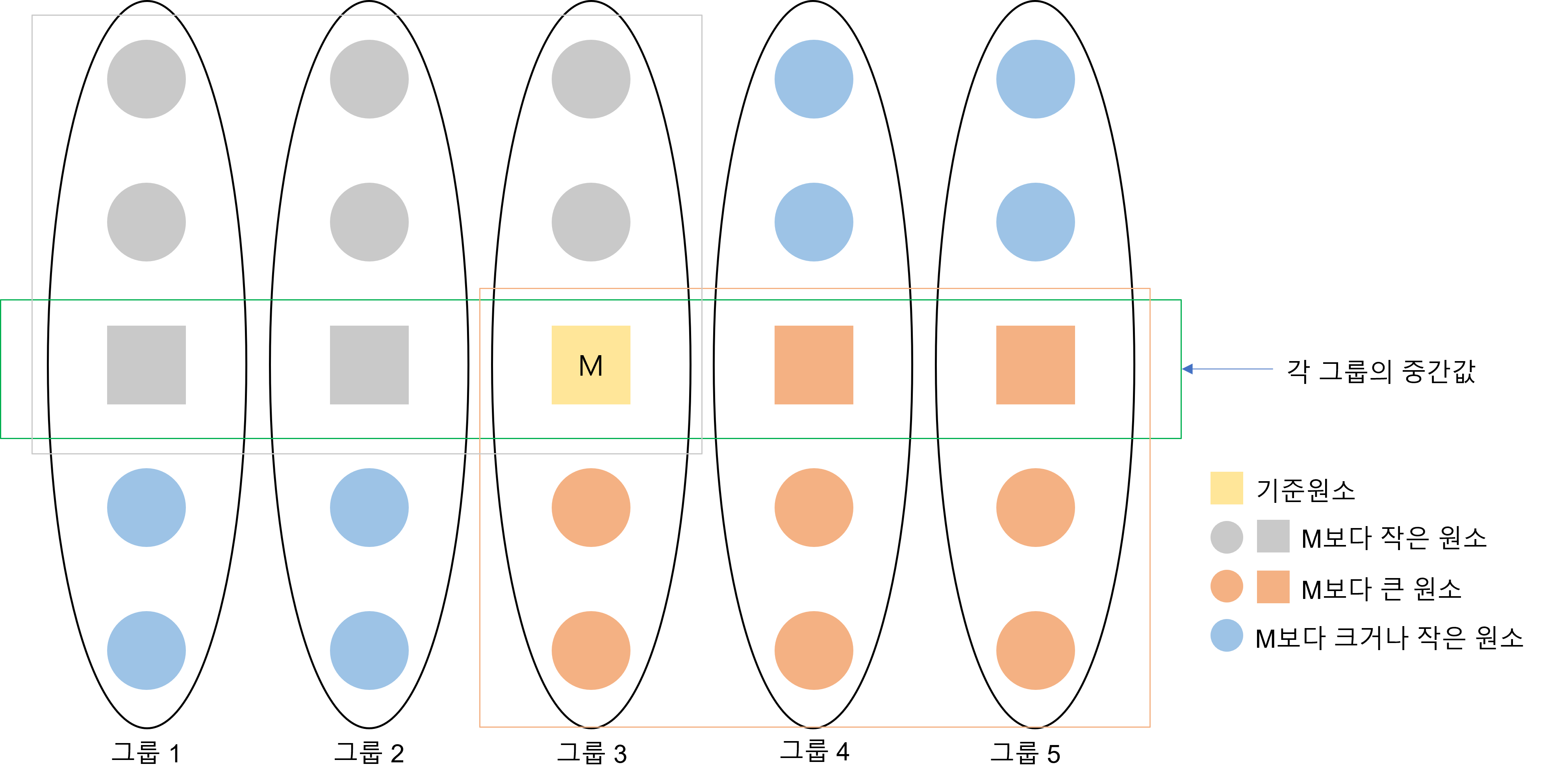
이 알고리즘의 최악의 경우는 위 그림에서 파란색 원소들이 모두 한곳으로 집중된 경우이다. 파란색 원소들이 모두 왼쪽으로 몰렸다고 가정한다면, 빨간색인 원소들은 적어도 \({3 \over 10}n - 3\)개씩 있다. 기준 원소인 M을 포함하게 된다면 \({3 \over 10}n - 2\)개가 된다. 이를 제외한 나머지 원소들의 수는 많아야 \({7 \over 10}n +2\)개가 된다. 즉, 최악의 경우는 이 \({7 \over 10}n +2\)개그룹에 속할 때이다. 이것만으로도 분할 비율은 최악의 경우에도 약 7:3임을 알 수 있다.
하지만, 이 분할의 비율을 어느 정도 보장되도록 하는 과정이 무시하지 못할 오버헤드가 든다. 위의 과정 1~4단계의 작업을 뜻한다. 1단계는 원소 수가 5개인 경우이면서 1번만 실행되므로 전체 실행시간에 영향을 주지 않는다. 2단계는 n개의 원소를 5개로 나누는 과정이므로 \(\Theta(n)\)의 시간이 소요된다. 3단계는 5개의 원소로 나누어진 그룹별로 상수시간이 소요된다. 4단계는 자기호출이다. 따라서 위 알고리즘의 실행 시간은 다음과 같다.
$$\begin{flalign}T(n) &\le T(\lceil{n \over 5}\rceil) + T({7 \over 10}n + 2) + \Theta(n) \\ &\le T({n \over 5} + 1) + T({7 \over 10}n + 2) + \Theta(n) &&\end{flalign} $$
\(n_0 \le k < n\)인 모든 \(k\)에 대해 \(T(k) \le ck\)라고 가정하자. (단, \(n_0\)는 \(7\)이상의 자연수)
$$\begin{flalign} T(n) &\le c({n \over 5}+1) + c({7 \over 10}n + 2) + \Theta(n) \\&= c({9 \over 10}n + 3) +\Theta(n) \\&= cn - {c \over 10}n + 3c + \Theta(n) &&\end{flalign}$$
이때, \(-{c \over 10}n > 3c + \Theta(n) \)을 만족하는 \(c\)가 존재한다.
따라서 \(T(n) \le cn \)이므로, \(T(n) = \Theta(n) \)이다.
\(n_0\)가 \(7\)이상인 이유
\(n\)보다 작은 \(k\)에 대해 \(T(k) \le ck\)라고 가정했으므로 아래의 식을 만족해야한다.
$$\begin{flalign} {1 \over 5}n + 1 < n \ and \ {7 \over 10}n + 2 < n &&\end{flalign}$$
이를 정리하면,
$$\begin{flalign} {20 \over 3} < n &&\end{flalign}$$
\(n\)은 자연수 이므로 \(7 \le n\)이다.
[Reference]
문병로, 「쉽게 배우는 알고리즘」 (한빛 아카데미, 2018)
'알고리즘(Algorithm) > Algorithm' 카테고리의 다른 글
| [알고리즘] 너비 우선 탐색(BFS) / 깊이 우선 탐색(DFS) (0) | 2022.04.04 |
|---|---|
| [알고리즘] 이진 탐색 트리 (0) | 2022.03.23 |
| [알고리즘] 정렬(3) - 기수 정렬, 카운팅 정렬 (0) | 2022.03.16 |
| [알고리즘] 정렬(2) - 병합 정렬, 퀵 정렬, 힙 정렬 (0) | 2022.03.15 |
| [알고리즘] 정렬(1) - 선택 정렬, 버블 정렬, 삽입 정렬 (0) | 2022.03.09 |