반응형
컴퓨터에서 탐색은 레코드(record)의 집합에서 특정한 레코드를 찾아내는 작업을 뜻한다. 레코드는 하나 이상의 필드(field)로 구성된다. 예를 들어, 한 학생의 정보를 구조체로 저장한다면, 구조체가 레코드고 이름, 학번, 학과 등등이 필드가 된다. 레코드를 서로 구별하기 위해서는 필드들 중에서 서로 중복되지 않는 고유한 값이 필요한데, 이를 키(key)라고 한다.
이진 탐색 트리는 다음과 같은 특징을 지니는 이진 트리이다.
1. 이진 탐색 트리의 각 노드는 키 값을 하나씩 가진다. 또한 각 노드의 키 값은 달라야한다.
2. 최상위 레벨에는 루트 노드가 있고, 각 노드는 최대 두 개의 자식 노드를 가진다.
3. 각 노드의 키 값은 왼쪽에 있는 모든 노드의 키 값보다 크고, 오른쪽에 있는 모든 노드의 키 값보다 작다.


[자료구조] 트리
트리 트리는 스택, 큐 등의 선형적인 자료구조가 아니라, 계층적인 구조의 자료구조이다. 컴퓨터의 폴더 구조, 가계도, 회사의 조직도 등 계층적인 관계들을 표현한 자료구조이다. 이 외에도 인
ggjjdiary.tistory.com
탐색
이진 탐색 트리에서 키가
1. 루트 노드의 키가이면 루트 노드를 반환한다. k
2.가 루트 노드의 키보다 작으면 왼쪽 서브트리로, 크면 오른쪽 서브트리로 탐색한다. k
3. 1-2의 과정을 반복해 키가인 노드를 찾는다. 만약 없다면 예외 처리를 해준다. k
// 노드 검색
Node* search(Node* n, int k) {
if (n == NULL) {
cout << "해당 값을 가진 노드가 없음" << endl;
return NULL;
}
if (n->data == k) {
return n;
}
else if (n->data > k) {
return search(n->left, k);
}
else {
return search(n->right, k);
}
}
삽입
삽입은 위에서 언급한 이진 탐색 트리의 특징을 위배하지 않는 선에서 이루어져야한다.
1. 탐색과 같은 방법으로 이진 탐색 트리에 해당 값이 있는지 찾는다.
2. 값이 없다면 마지막으로 찾은 노드의 자식 노드로 한다.
물론 해당 트리가 공백 상태라면
// 노드 삽입
void insert(Node* r, Node* n) {
if (r->data == n->data) {
cout << "이미 해당 값을 가진 노드가 있음" << endl;
return;
}
else if (r->data > n->data) {
if (r->left == NULL) {
r->left = n;
}
else {
insert(r->left, n);
}
}
else {
if (r->right == NULL) {
r->right = n;
}
else {
insert(r->right, n);
}
}
}
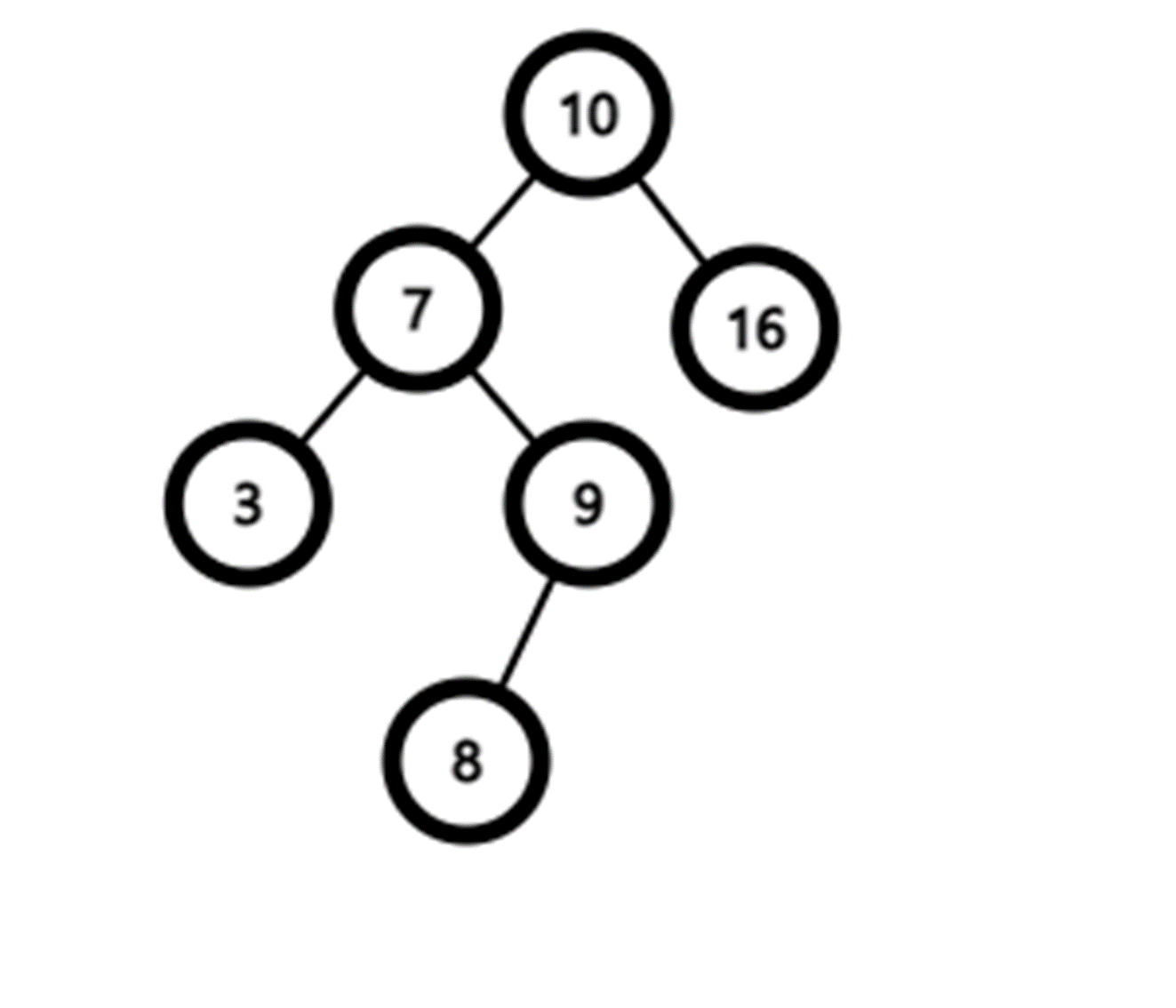
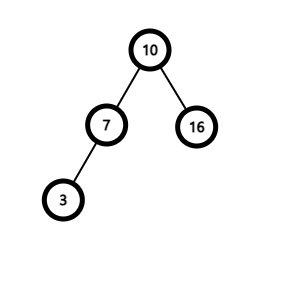
삭제
키가 k인 노드 n을 삭제한다고 해보자. 삭제는 3가지 경우에 따라 달라진다.
n이 리프 노드인 경우
부모노드에서 n의 링크를 끊어 NULL과 연결한다.

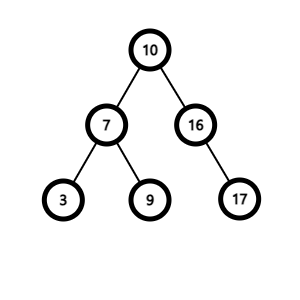
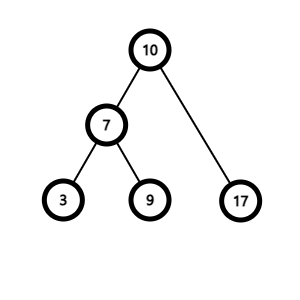
n의 자식노드가 하나인 경우
n을 삭제하고 n의 부모노드를 n의 자식노드에 연결한다.
n의 자식노드가 두 개인 경우
1. n이 있던 자리에 옮겨도 이진 탐색 트리의 성질을 깨지 않는 노드를 찾는다.
(n의 왼쪽 서브트리에서 키 값이 가장 큰 노드이거나, 오른쪽 서브트리에서 가장 작은 노드가 해당된다.)
2. 해당 노드를 n의 위치로 옮긴다.
3. 해당 노드가 자식 노드가 있었다면 자식 노드를 연결해준다.
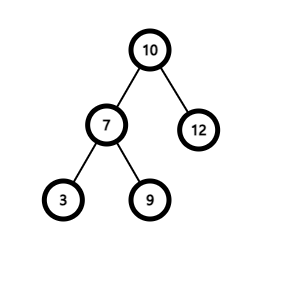
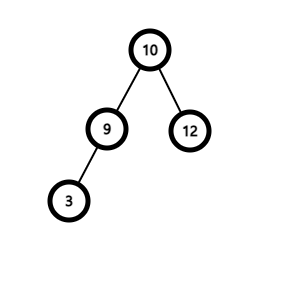
// 노드 삭제
void remove(Node* p, Node* n) {
Node* child, *successor, * successor_p;
// n이 리프 노드인 경우
if (n->left == NULL && n->right == NULL) {
if (n == root) { // n이 루트 노드일 경우.
root = NULL;
}
else {
if (p->left == n) {
p->left = NULL;
}
else {
p->right = NULL;
}
}
}
// n의 자식노드가 하나인 경우
else if (n->left == NULL || n->right == NULL) {
if (n->left == NULL) {
child = n->right;
}
else {
child = n->left;
}
if (n == root) {
root = child;
}
else {
if (p->left == n) {
p->left = child;
}
else {
p->right = child;
}
}
}
// n의 자식노두가 두 개인 경우
else {
successor_p = n; // 후계자의 부모노드 (이하 후부모노드)
successor = n->right; // 후계자 노드
// 오른쪽 서브트리의 가장 작은 노드를 탐색
while (successor->left != NULL) {
successor_p = successor;
successor = successor->left;
}
// 후부모노드의 왼쪽 자식노드가 후계자면
if (successor_p->left == successor) {
// 후부모노드의 왼쪽 자식으로 후계자의 오른쪽 자식노드를 연결
successor_p->left = successor->right;
}
// 그렇지 않으면 후부모노드의 오른쪽 자식으로 후계자의 오른쪽 자식을 연결
else {
successor_p->right = successor->right;
}
n->data = successor->data; // n의 값을 후계자로 변경
n = successor; // n이 후계자 노드를 가리킴
}
delete n;
}
[Reference]
문병로, 「쉽게 배우는 알고리즘」 (한빛 아카데미, 2018)
728x90
'알고리즘(Algorithm) > Algorithm' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리(Minimum Spanning Tree) (0) | 2022.04.04 |
|---|---|
| [알고리즘] 너비 우선 탐색(BFS) / 깊이 우선 탐색(DFS) (0) | 2022.04.04 |
| [알고리즘] 선형 시간 선택 알고리즘 (0) | 2022.03.18 |
| [알고리즘] 정렬(3) - 기수 정렬, 카운팅 정렬 (0) | 2022.03.16 |
| [알고리즘] 정렬(2) - 병합 정렬, 퀵 정렬, 힙 정렬 (0) | 2022.03.15 |