미숙한 블로그 주인이 코딩테스트 문제를 풀어가는 과정을 담은 글입니다. 이 풀이가 효율적인 풀이가 아닐 수 있으며, 부정확한 정보가 많이 있을 수 있습니다. 보완해야할 점이 있다면 댓글로 남겨주세요!
https://programmers.co.kr/learn/courses/30/lessons/12953#
코딩테스트 연습 - N개의 최소공배수
두 수의 최소공배수(Least Common Multiple)란 입력된 두 수의 배수 중 공통이 되는 가장 작은 숫자를 의미합니다. 예를 들어 2와 7의 최소공배수는 14가 됩니다. 정의를 확장해서, n개의 수의 최소공배
programmers.co.kr
N개의 최소공배수
문제
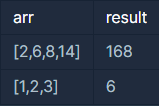
두 수의 최소공배수(Least Common Multiple)란 입력된 두 수의 배수 중 공통이 되는 가장 작은 숫자를 의미합니다. 예를 들어 2와 7의 최소공배수는 14가 됩니다. 정의를 확장해서, n개의 수의 최소공배수는 n 개의 수들의 배수 중 공통이 되는 가장 작은 숫자가 됩니다. n개의 숫자를 담은 배열 arr이 입력되었을 때 이 수들의 최소공배수를 반환하는 함수, solution을 완성해 주세요.
제한사항
- arr은 길이 1이상, 15이하인 배열입니다.
- arr의 원소는 100 이하인 자연수입니다.
풀이
입출력 예시
풀이
보통 최소공배수를 구할 때 소인수 분해를 사용하거나 나눗셈을 이용할 것이다. 처음에는 나도 나눗셈을 이용해서 풀어봤다.
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int solution(vector<int> arr) {
int answer = 1;
int prime_factor = 2;
int max_num = 0;
int prime_count = 0;
vector<int> prime_list;
for (int i = 0; i < arr.size(); i++) { // 가장 큰 수를 찾는다.
max_num = max(max_num, arr[i]);
}
if (max_num == 1 || arr.size() == 1) { // 만약 가장 큰 수가 1이거나 크기가 1이면
return max_num; // 최댓값을 반환
}
while (prime_factor <= max_num) {
prime_count = 0;
for (auto& a : arr) {
if (a % prime_factor == 0) { // '공'배수를 구해야 하므로 공통 인수여야 한다.
prime_count++;
}
}
if (prime_count < 2) { // '공'배수를 구해야 하므로 공통 인수가 아닌 것은 제외
prime_factor++;
continue;
}
prime_list.push_back(prime_factor);
for (auto& a : arr) { // 해당 인수를 가지는 모든 수에 대해 인수로 나눠준다.
if (a / prime_factor == 0) {
if (a == max_num) {
max_num = a;
a = 1;
}
else {
a = 1;
}
}
else if (a % prime_factor == 0) {
if (a == max_num) {
a /= prime_factor;
max_num = a;
}
else {
a /= prime_factor;
}
}
}
}
for (const auto& a : arr) { // 나머지가 끝난 뒤 남은 수들과 인수들을 곱해준다.
answer *= a;
}
if (prime_list.size() > 0) {
for (const auto& p : prime_list) {
answer *= p;
}
}
return answer;
}테스트 케이스가 잘 돌아가길래 바로 제출을 눌렀다. 그런데,,
빨간색이 이렇게 많은건 처음 봤다... 접근 방법이 잘못 되었거나, 알고리즘에 실수가 있는 것이 분명했다.. 접근 방식이 잘못 되었을까 싶어서 과감히 초기화를 누르고, 재귀 호출을 이용해서 알고리즘을 수정해봤다.
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int get_lcm(vector<int> arr, int cm) {
bool is_prime = false;
int lcm = cm;
int max_num = 0;
for (int i = 0; i < arr.size(); i++) {
max_num = max(arr[i], max_num);
}
if (cm == 1 || arr.size() == 1) {
return cm;
}
for (int i = 2; i <= max_num; i++) {
int tmp;
if (lcm % i == 0) {
tmp = lcm / i;
// tmp가 a로 나누어 떨어지면 이 또한 공배수이다.
for (const auto& a : arr) {
if (tmp % a != 0) {
is_prime = false;
break;
}
else {
is_prime = true;
}
}
}
if (is_prime) { // 또다른 공배수를 찾았으면 이 수를 이용해서 처음부터 다시 찾아본다.
return get_lcm(arr, tmp);
}
}
return lcm;
}
int solution(vector<int> arr) {
int answer = 0;
int lcm = 1;
for (const auto& a : arr) {
lcm *= a;
}
return answer = get_lcm(arr, lcm);
}이번에는 다른 방식이었다. 원소들을 다 곱한 뒤에, 작은 수에서 부터 나눠가다가, 모든 원소랑 나누어떨어지면 그 수를 가지고 다시 처음부터 나눠가는 방식이다. 정말 무식한 방법이었다. 이런 무식한 방식에 대한 답변은...
실패였다. 한숨이 절로 나온다. 다시 생각해보자. 혹시, 내가 몰랐던 최소공배수를 구하는 다른 방법이 있는 것이 아닐까? 검색해보니, 다른 방법이 정말로 있었다. 유클리드 호제법을 이용한 방법.
https://ko.wikipedia.org/wiki/%EC%9C%A0%ED%81%B4%EB%A6%AC%EB%93%9C_%ED%98%B8%EC%A0%9C%EB%B2%95
유클리드 호제법 - 위키백과, 우리 모두의 백과사전
유클리드 호제법(-互除法, Euclidean algorithm) 또는 유클리드 알고리즘은 2개의 자연수 또는 정식(整式)의 최대공약수를 구하는 알고리즘의 하나이다. 호제법이란 말은 두 수가 서로(互) 상대방 수를
ko.wikipedia.org
2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다.
설명만 들으면 이해가 안 간다. 예시를 보자.
1071과 1029의 최대공약수를 구하면,
1071은 1029로 나누어 떨어지지 않기 때문에, 1071을 1029로 나눈 나머지를 구한다. ≫ 42
1029는 42로 나누어 떨어지지 않기 때문에, 1029를 42로 나눈 나머지를 구한다. ≫ 21
42는 21로 나누어 떨어진다.
따라서, 최대공약수는 21이다.
아! 이제 감이 잡힌다. a와 b로 나누었을 때, 나누어 떨어지지 않는다면, 그 나머지(r)과 b를 이용해서 다시 앞의 과정을 반복하는 것이다.
int euclidean_algorithm(int a, int b) {
int r;
if (a % b == 0) {
return b;
}
else {
r = a % b;
return euclidean_algorithm(b, r);
}
}그런데, 이것을 최소공배수에 어떻게 이용하는가 했더니... a x b = 최소공배수 x 최대공약수 였다. 그러니까, 최대공약수만 알면 최소공배수를 바로 알 수 있게 된다. 그러나, 내가 구해야 할 것은 입력이 2개인 경우가 아니라 3개 이상이 될 수도, 1개일 수도 있었다. 나는 혹시? 라면서 메모장에 끄적여봤다.
5라는 수가 들어오면, a = 1로 b = 5로 하면?
최대공약수는 1에, 최소공배수는 5로 나온다.
4, 6, 9 라는 수가 들어오면?
1. a = 4, b = 6으로 하면 gcd = 2, lcm = 12
2. 직전에 구했던 최소공배수인 12와 9를 각각 a, b로 하면 gcd = 3, lcm = 36
4, 6, 9의 최소공배수는 36이다.
두개씩 합쳐서 계산해도 결과는 맞게 떨어졌다!
바로 위의 과정을 코드로 옮겨봤다.
int solution(vector<int> arr) {
int answer = 1;
for (int i = 0; i < arr.size(); i++) {
answer = (arr[i] * answer) / euclidean_algorithm(answer, arr[i]);
}
return answer;
}전체 코드
#include <vector>
using namespace std;
int euclidean_algorithm(int a, int b) {
int r;
if (a % b == 0) {
return b;
}
else {
r = a % b;
return euclidean_algorithm(b, r);
}
}
int solution(vector<int> arr) {
int answer = 1;
for (int i = 0; i < arr.size(); i++) {
answer = (arr[i] * answer) / euclidean_algorithm(answer, arr[i]);
}
return answer;
}결과
코딩 테스트 덕분에 새로운 공식을 하나 알아간다.
'코딩 테스트(Coding test) > Lv. 2' 카테고리의 다른 글
| [프로그래머스/C++] JadenCase 문자열 만들기 (0) | 2022.03.19 |
|---|---|
| [프로그래머스/C++] 피보나치 수 (0) | 2022.03.19 |
| [프로그래머스/C++] 행렬 테두리 회전하기 (0) | 2022.03.16 |
| [프로그래머스/C++] 예상 대진표 (0) | 2022.03.14 |
| [프로그래머스/C++] 영어 끝말잇기 (0) | 2022.03.13 |